سوالات ریاضی

[ماهرو]

اثبات این رو میدونید؟
فرض:
a<b+c
b<a+c
c<a+b
حکم:
b_c|<a<b+c|

 

[امین]

اثبات این رو میدونید؟
فرض:
a<b+c
b<a+c
c<a+b
حکم:
b_c|<a<b+c|

ببین کافیه دو به دو این رابطه‌ها رو از هم کم کنی
b<a+c
c<a+b
نتیجه‌ی تفاضل این دوتا از هم این میشه
b-c<c-b
2b<2c
b<c
حالا برای دو رابطه‌ی دیگه این کارو انجام میدی
a-b<b-a
2a<2b
a<b
در کل به چنین رابطه‌ای می‌رسی که a<b<c
پس بدیهیه وقتی a از b کوچیک‌تره و خود b هم از c کوچیک‌تره پس a از مجموع b و c هم کوچیک‌تر میشه؛ پس یعنی یک سمت حکم ثابت شد a<b+c
از طرفی ما بنا به فرض داشتیم c<a+b و این یعنی اگه b رو به اون سمت ببریم میشه c-b<a و چون b از c کوچیک‌تره، می‌تونیم به طور کلی اعلام کنیم b-c هم کوچیک‌تر از a عه، و این یعنی قدرمطلق تفاضل b و c در هر حالتی از a کوچیک‌تره و طرف دیگه‌ی حکم هم به اثبات می‌رسه.

 

[sicario]

یک چهار ضلعی محدب با قطر های 6و7 داریم.
محیط چهار ضلعی کدام میتواند باشد؟
1) 15
2)10
3)27

 

[sicario]

1

خو چرا؟

 

[sicario]

2؟

اینم اثبات کنی ممنونت میشم
بعد کلاست

 

[sicario]

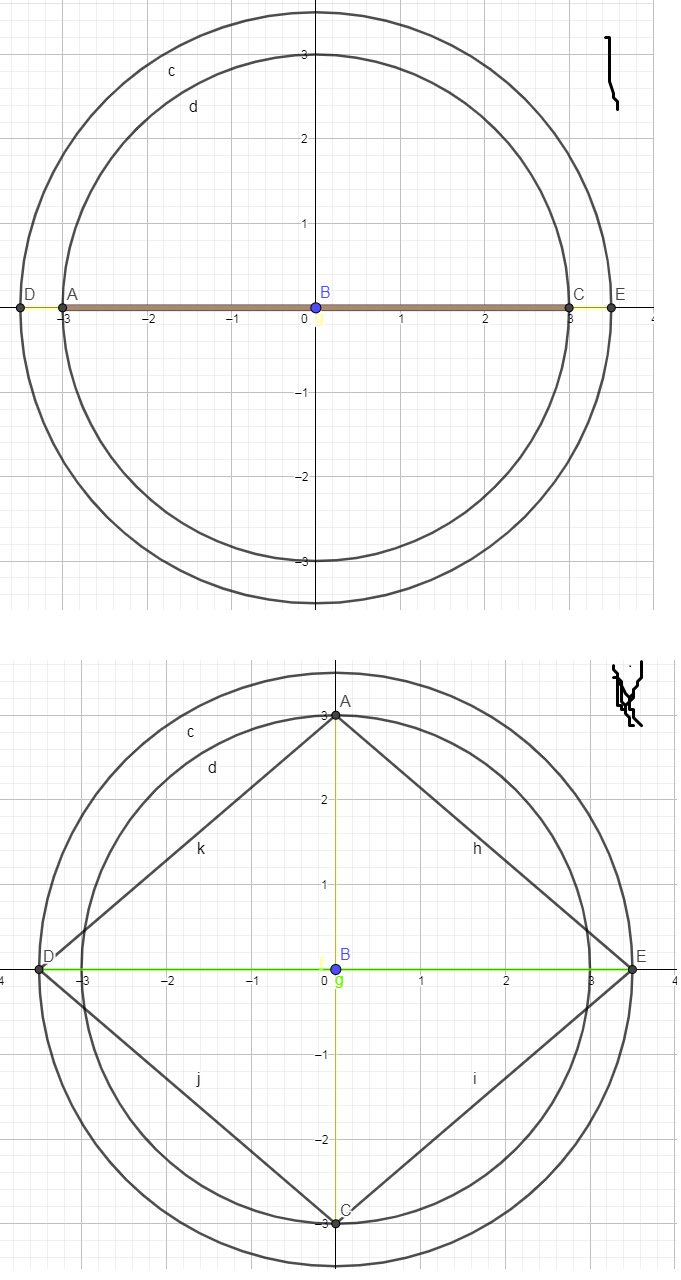
تو حالت 1 که دو تا قطر روی هم افتادن و زاویه بینشون صفره هیچ اتفاق خاصی نمیوفته اما اگه یکمی زاویه بیشتر بشه چهار ضلعی تشکیل میشه و حساب کردن محیطش دردسره پس برای حالت 1 مجموع دو قطر یا همون 13 رو در نظر میگیریم


تو حالت دوم هم که حداکثر زاویه رو دارن محیطش تقریبا میشه 18.04 (طول یک ضلع * چهار که با فیثاقورث درمیاد)

پس محیط میتونه بین اینا باشه
13<x< هیجده


حالا جواب درسته یا دارم چرت و پرت میبافم؟

شک م هم این بود که اگه منصف هم نباشن چی و دیدم حالت های زیادی هست

ببین فکر کنم که راه حلت خییلی درست نیست. به همون دلیلی که تو خط اخر گفتی
من این شکلی رفتم که مطمئن تره(اون نامساوی ها از اصل حمار استفاده شده) :

 

[./.]

اینم اثبات کنی ممنونت میشم
بعد کلاست

حاصل جمع مطلوب عبارتست از جمع مجموعه کسرهایی که صورتشان 1 و مخرجشان شمارنده های آن عدد از جمله خود آن عدد اند. پس مخرج مشترک را خود آن عدد میگیریم و صورت ها هرکدام باید در حاصل تقسیم آن عدد بر خود -که عبارتست از شمارندۀ دیگری از آن عدد- ضرب شوند و از آنجا که صورت ها یک اند، پس صورت کسر حاصل عبارت خواهد شد از تمام شمارنده های آن عدد. -زیرا هر شمارنده از تقسیم آن عدد بر شمارندۀ متناظر به دست می اید. مثلا در مثال 6، 2 از تقیم 6 بر 3 پیش می اید و 3 برعکس- حال چون عدد کامل است، مجموع شمارنده های کوچکتر از خودش برابر با خودش خواهند شد و خودش هم که در صورت حضور دارد، پس دو برابر خود عدد در صورت است و خودش هم که در مخرج بود، پس حاصل 2 خواهد شد.

 

[Lushato]

در برابر سوالای شما که چیزی نیست
ولی خب نمیدونم چیکارش کنم....

 

[sicario]

در برابر سوالای شما که چیزی نیست
ولی خب نمیدونم چیکارش کنم....

مساحت مربع که x^2 هست
مساحت دایره هم p*r^2
حالا برای مساحت دایره به جای r، مقداری که بر حسب ایکس داده رو جای گذاری میکنی
تهش این دوتا رو باهم جمع میکنی
یه عبارتی بهت میده بر حسب x که عبارته مساویه 6 هست
که بعد میتونی از اون x رو بدست بیارید
اگه بازم سوال داشتید بگید که عکس بگیرم بفرستم

در برابر سوالای شما که چیزی نیست
ولی خب نمیدونم چیکارش کنم....

?

 

[sicario]

?

حالا یه مرحله جلوتر:

?
پ ن: ترجیحا دانشگاهی ها حل نکنن، بزارن برای دبیرستانی ها یه چالشی بشه!